How To Find The Slope Of Line On A Graph

An online slope estimator helps to detect the slope (m) or slope betwixt 2 points $A$ $(x_1, y_1)$ and $B$ $y_1, y_2)$ in the Cartesian coordinate plane. This gradient of a line calculator volition take two points to calculate $(m)$ and $y-intercept$ of a line.

In mathematical terms, the gradient or gradient of the line is said to be a number that defines both the direction and steepness of the line. Typically, it is denoted past the letter $(m)$.

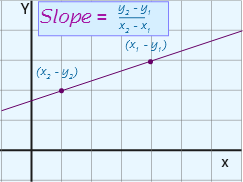
slope formula

There are four different types of slope that all are depending on the direction of the line. Read on!

If the line goes up to the right, it is said to be a positive slope or gradient
If the line goes down to the right, the it is said to be a negative slope or gradient
A horizontal line has a slope $(m)$ of zero
A vertical line has an undefined slope or gradient

You can effort our slope finder that allows you to find both $10-intercept$ and $Y-intercept$ from the given points.

Requite a endeavour to this best midpoint calculator online that enables to find the distance & midpoint of a line segment and also shows you the step-by-step consummate calculations.

Also, the gratis slope intercept form calculator by calculator-online helps to find slope-intercept form equation from given points.

Slope Calculator Helps To Practice:

This estimator allows you to perform calculations corresponding to the slope and dissimilar other parameters:

You tin readily notice $(yard)$ or gradient of a line that passes through 2 points
It assists you to solve a coordinate for a given signal, $(thousand)$ or angle $(θ)°$, and altitude from a point
Information technology helps yous to discover the $x$ or $y$ of a betoken for a given another point and the $(thousand)$ or angle $(θ)°$
You lot can readily find $(m)$ or bending for a given parameters
It allows you to notice the slope of the given line

Well, in this post, nosotros are going to tells y'all what is the slope formula is, how to discover it (manually) or by using a estimator, and much more.

Also, use this free point slope form estimator online that displays the equation of a line by using the coordinate points and $(m)$ of the line.

What is The Slope Formula:

$$ Slope (m) = \frac {ΔY}{ΔX} or \frac {y_2 – y_1} {x_2 – x_1} $$

In this gradient equation;

$m$ = $slope$

$ΔY$ = $(y_2 – y_1)$

$ΔX$ = $(x_2 – x_1)$

Teachers frequently use different words for the y-coordinates and the 10-coordinates:

Some refer to $y-coordinates$ as the $rise$ and $ten-coordinates$ as the $run$
Others consider the $Δ$ notation and refer to the $y-coordinates$ as $Δy$, and $x-coordinates$ every bit $Δx$

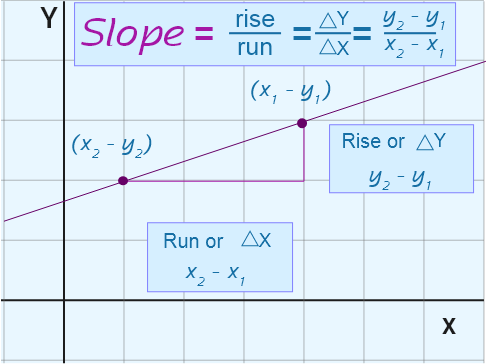
calculate slope

Slope Example:

Let's use the above formula to find the gradient that goes through the points $(2, 1)$ and $(4, seven)$.

Pace # 1:

Starting time of all, you lot take to identify the values of $x_1, x_2, y_1$ and $y_2$.

$x_1) = two$

$y_1 = 1$

$x_2 = iv$

$y_2 = vii$

Stride # 2:

Now, you have to put the above values into the formula:

$(m)$ = $\frac {y_2 – y_1}{x_2 – x_1} = \frac {7 – 1} {4 – ii} = \frac {six}{2} = three$

Step # iii:

Get check the result and y'all ought to make sure that this slope make sense by thinking about the points on the coordinate plane.

Also, you can try this formula (g=y2-y1/x2-x1 reckoner) to find the gradient of the line or given coordinates.

How to Detect Slope With This Slope Calculator:

The slope formula calculator uses the simple and smart formula for $(m)$ or gradient to do calculations.

Yous can perform calculations with the following:

Two Points:

Input:

First of all, you ought to select the 'two points' selection from the drib-down menu of this gradient solver for two points
Very next, you lot have to enter the $X_1$ value into the designated field
Then, you have to enter $Y_1$ value into the designated field
Right after, you take to enter $X_2$ value into the designated field
Now, you have to enter $Y_2$ value into the designated field

Output:

Once you entered all the above parameters, then simply striking the calculate button, the calculator helps to find slope from two points and generate:

Slope $(k)$
Percentage Grade
Angle $(θ)$
Distance
$ΔX$
$ΔY$
$X – Intercept$
$Y – Intercept$
Gradient-Intercept: $y = mx + b$
Graph For a 2 points

One Indicate, Gradient (m) or Angle (θ)° & Distance:

Input:

Showtime of all, you ought to select the 'One Point, Gradient $(g)$ or Angle $(θ)°$ & Distance' from the drop downward menu
Then, you have add the value of $X_1$ into the given field of the above computer
Very side by side, you lot have to add the value of $Y_1$ into the given field
Now, you ought to add the value for Slope $(thou)$ or Bending $(θ)°$ into the given field of this tool
So, yous ought to add the value of distance into the designated field

Output:

Once done, and then simply hitting the calculate push button:

Correct $X_2$
Correct $Y_2$
$ΔX$
$ΔY$
Graph for a right $X_2$ and right $Y_2$
Left $X_2$
Left $Y_2$
$ΔX$
$ΔY$
Graph for a left $X_2$ and left $Y_2$
Slope $(thou)$
Percentage Course
Angle $(θ)$
Distance
$X – Intercept$
$Y – Intercept$
Gradient-Intercept: $y = mx + b$

One Point, X or Y & Gradient (m):

Input:

At first, you ought to enter the value of $X_1$ into the given field
Then, yous ought to add the $Y_1$ value into the given box of the reckoner
Very adjacent, you lot ought to $X_2$ or either $Y_2$ into the given field
Now, you ought to add the Slope $(grand)$ or either Angle $(θ)°$ into the designated box

Output:

Once you added all the in a higher place-parameters, hit the summate button, this $(y=mx+b)$ calculator will generate:

$X_2$
$Y_2$
$Δx$
$Δy$
Slope $(m)$
Percentage Course
Bending $(θ)$
Distance
$10 – Intercept$
$Y – Intercept$
Gradient-Intercept: $y = mx + b$

Ane Signal & Slope (k):

Input:

At commencement, you have to enter the value of $X_1$ into the given field
Now, you have to add together the value of $Y_1$ into the given box
And so, just, yous have to enter $(m)$ or either Angle $(θ)°$ into the given field of slope finder

Output:

Once you filled the all parameters, then but hitting the calculate button, this figurer will generate:

Slope $(m)$
Percent Form
Angle $(θ)$
$X – Intercept$
$Y – Intercept$
Gradient-Intercept: $y = mx + b$

Line:

Input:

You have to enter a line equation into the given fields of this calculator

Output:

Once yous entered the line equation, and so hitting the calculate button, this volition generate:

Slope $(thousand)$
Percentage Grade
Angle $(θ)$
$10 – Intercept$
$Y – Intercept$
Slope-Intercept: $y = mx + b$

How To Find The Slope of a Line Given two Points?

Y'all tin find slope of a line by comparison any 2 points on the line. Wait at the given example for amend understanding:

Gradient Formula: $thou = \frac {y_2 – y_1}{x_2 – x_1}$

For Example:

The line passes through the points $(3, 2)$ and $(7, 5)$, how to find gradient of a line?

Solution:

$chiliad = ((v – 2))/((7 – 3))$

$chiliad = ((3))/((4))$

This estimator for slope helps you in finding the gradient or $(1000)$ and shows you the slope graph corresponding to the given points.

How to Detect The Distance Between 2 Points?

The formula to decide the distance (D) between 2 different points is:

$ Distance (d) = \sqrt {(10₂ – x₁)^2 + (y₂ – y₁)^ii } $

How to Convert Gradient to Angle?

You tin detect the angle of a line in degree from the inverse tangent of the slope $(k)$.

The Formula is:

$θ = tan-ane(1000)$

OR $θ = arctan \frac {(ΔY)}{(ΔX)}$

Where;

$m$ = gradient

$θ$ = angle of incline

For Example:

If the gradient is 5, the angle of an incline in degrees is tan-i(5).

How to Catechumen Bending to Slope?

Simply, all you have to remember is that the slope is equal to the tangent of the angle.

Equation:

$k = tan(θ)$

For Example: If $angle = 90$, then the slope is equal to $tan (ninety)$.

Using The Linear Equation Course – how do you find y=mx+b?

As we know, the linear equation: $y = mx + b$, or sometimes $y = mx + c$,

Slope Equation of a Line:

$y = mx + b$, or sometimes $y = mx + c$,

where;

$m$ = slope (said to be the amount of rise over run of the line)
$b$ = $y-axis$ intercept (said where the line crosses over the $y-axis$

How to Detect the Equation of a Line From 2 Coordinates:

If you want to calculate the equation of a line from two coordinates $(x_1, y_1)$ and $(x_2, y_2)$ manually, and then yous have to stick to the post-obit steps:

Step # ane:

First of all, you have to use the $(m)$ formula to calculate the slope $\frac {(y_2 – y_1)}{(x_2 – x_1)}$

Step # 2:

At present, you ought to calculate where the line intersects with the $y-centrality$:

To practise and then,

You lot ought to enter i of the coordinates into this slope equation: $y – mx = b$

Case:

Want to calculate the slope-intercept equation for a line, which includes the ii points i:due east $(7, 4)$ and $(i, ane)$, allow'due south have a look!

Stride # ane:

Slope $(k)$ = $\frac {ΔY}{ΔX} = \frac {(1 – 4)}{(1 – 7)} = \frac {(-3)}{(-half dozen)}$

Slope $(m)$ = $\frac {-3}{-6} = \frac {1}{2}$

Step # 2:

And so, at present, using ane of the original coordinates $(seven, four)$, nosotros readily find the $y-axis intercept (b)$ using the gradient formula:

$y – mx = b$

$y=4, chiliad=\frac {1}{2}, 10 =7$

$y – mx = b$

$b= .5$

The slope equation for this line is equally:

$y = .5x + .v$

This line crosses the $y-axis$ at $.5$ and has a gradient of $.5$, then it referred to as this line rises one unit along the $y-axis$ for every $2$ units it moves along the $x-axis$. Besides, our online computer show the same answer for these given parameters.

How to Find a Point Given ane Point, Slope(m), and Altitude:

No doubt, points on a line tin can be readily solved given the slope of the line and the distance from another bespeak. The formulas to detect 10 and y of the point to the right of the signal are every bit:

$ x_2 = x_1 + \frac{d}{\sqrt(1 + thousand^2)} $
$ y_2 = y_1 + m \times \frac{d}{\sqrt(1 + m^2)} $

The formula's to find x and y of the betoken to the left of the point are equally:

$ x_2 = x_1 + \frac{-d}{\sqrt(1 + chiliad^two)} $
$ y_2 = y_1 + k \times \frac{-d}{\sqrt(i + thousand^2)} $

How to Solve the (Δ) Delta of 10 and y:

The symbol $Δ$ is used to express the delta of $ten$ and $y$, simply, it is the accented value of the distance between $x$ values or $y$ values of $2$ points.

The $(Δ)$ delta of $x$ can be adamant using the formula:

$Δx = x_2 – x_1$

The $(Δ)$ delta of y can be determined using the formula:

$Δy = y_2 – y_1$

When Slope and 1 Point Are Known:

Let'due south take a expect!

Example:

A line is passes through the point $(7,5)$ and it has a gradient of $9$. What is the equation?

Well, we can hands calculate $'b'$ from this equation:

$b = y – mx$

At present, let's plug-in the values into the higher up equation:

$b = five – (ix)(vii)$

$b = -58$

Very next, we plug-in the value of $'b'$ and the gradient into the given equation:

$y = mx +b$

$y = 9x -58$

Also, you can utilise the to a higher place slope finder to perform instant calculations instead of sticking to these manual calculation steps!

FAQ's:

How do yous calculate a 2% slope?

Slope as a Percentage:

Yes, gradient or $(m)$ can be adamant as a percentage that is calculated in much the same as the gradient. Simply stick to the following steps to reach best!

Showtime of all, you have to catechumen the rise and run to the aforementioned units
Then, you take to dissever the rise by the run
Now, you ought multiply this number past $100$, means y'all take the pct slope

For instance:

$"2"$ ascension divided by $"24"$ $run$ = $.083 \times 100$ = an $8.3%$ slope.

What is a ane% slope in inches?

Simply, $i%$ equally a decimal is $0.01$ and hence the gradient is referred to as $0.01$. Means that for a run of pipe of a certain length the rise should be $0.01$ times the length. Thus a, for instance, equally the length of the run is $eighty$ feet that is expressed equally $80 \times 12 = 960$ inches the rise should be $0.01 \times 960$ $= nine.6 inches$.

What is the slope of 1/4 inch per foot?

$1/4″$ per foot pitch equals to $ii%$ $(percent)$, and remember that it is not expressed as $2$ degrees.

What is a 20% gradient?

$Slope per centum$ $=$ $\frac {8 feet}{40 anxiety} \times 100 = 0.twenty \times 100 = 20%$

What is the slope of y =- 4x 3?

In this equation, the slope is expressed as $−4$ as this equation is in standard linear form that is $y=mx+c$, where $g$ is the slope.

How do I find a gradient with no points?

Only, yous ought to apply a protractor and trigonometry!

Tin can I find the slope of -1?

When information technology comes to a straight line with a slope of $-one$, it moves down at a $45°$ angle as it moves to the right.

How do you calculate the slope of a hill?

All you lot need to simply divide the elevation modify in anxiety by the distance of the line that you drew (after converting it to anxiety). Then, you demand to multiply the resulting the number by 100 to discover a percentage value equal to the pct slope of the hill.

How do you lot summate the length of a slope?

You lot need to utilise the Pythagorean Theorem to summate the length of a slope, where the vertical distance is said to exist ascension and the horizontal distance indicated every bit the $run: rise^2 + run^2 = slope length^2$.

What is a 1 in xx slope?

The maximum running slope allowed is $ane:20$ for the parts of an accessible route that aren't a ramp. Simply, it means that for every inch of height modify there should be at-least $20in$ of route run. Also, the distance from the bottom border of the level to the surface volition not exist more than $1.2 inches (1.2:24 = 1:20)$.

How do you lot find the slope of a curve?

When information technology comes to finding the slope $(thousand)$ of a bend at a particular point, you need to differentiate the equation of the curve. If the given curve is $y = f(x), y = f(x)$, you ought to evaluate $\frac{dy}{dx}$ and substitute the value of $10$ to calculate the slope.

Is charge per unit of change the same as slope?

When y'all're going to find the slope of real-world situations, typically it is referred to as the charge per unit of alter. Recollect that "Charge per unit of alter" indicates aforementioned as $"m"$. If you are asked to observe the rate of modify, simply use the $(m)$ formula or make a slope triangle.

Where do you employ slope in everyday life?

Remember that slope is a measure of steepness. Some existent-life examples of slope are mentioned-below:

To building roads when you need to know how steep the road will be
Skiers/Snowboarders consider the slopes of hills as it helps to judge the dangers, speed, etc
When it comes to amalgam wheelchair ramps, gradient is a major consideration
When it comes to building stairs, you should take to consider the slope then that they are not too steep to walk on
In art, slopes of the line should considered as information technology assists to decide what would exist the almost aesthetically pleasing to center

What is a 10% gradient?

A $10%$ slope indicates that, for every $100 ft (feet)$ of horizontal distance, the altitude simply changes by $10 ft (anxiety): {10 ft over 100 ft} \times 100 = 10%$.

How to find the area under a slope?

Yous should accept to integrate the equation & subtract the lower bound of the area from the upper jump to find the area under a gradient. When it comes to linear equations:

First of all, you need to put the equation into the course $y=mx+c$
At present, you ought to write a new line where you lot ought to add $1$ to the order of the $x$ (for instance, $10$ becomes $x2, x2.v$ becomes $x3.five$
Very side by side, you demand to divide slope $(yard)$ by the new number of the order and place it in forepart of the new $x$
And then, you ought to multiply the $c$ by $10$ and simply add this to the new line
Now, y'all ought to solve this new line twice: ane where $x$ is indicated as the upper jump of the expanse you need to observe and 2d where $10$ is indicated as the lower jump
Finally, subtract the lower spring from the upper leap
Congrats, you calculated expanse nether a slope

Takeaway:

Luckily, you lot come to know how to detect the slope manually in legitimate ways. The amazing thing is that there is no demand to remember these formulas, y'all just have to account the to a higher place $(m)$ slope calculator to find gradient or $(thou)$.

References:

From Wikipedia, the gratuitous encyclopedia – what is the slope – Examples and much more!

The Source of Mathplanet recently updated – Pre-Algebra / Graphing and functions / – how to find (m) –

From the source of mathblog – An Introduction To Algebra – Solve for Slope with 2 Points on a Line

The coolmath provided you with – Algebra – Page 1 of 2 – Finding the Slope of a Line from the Equation – The Globe of Math

Other Languages: Steigung Berechnen, 勾配計算, Calcul Pente, Calculo De Inclinação, Calcular Pendiente, Calcolo Pendenza, Калькулятор Уклонов, Výpočet Sklonu, Kattokaltevuus Laskuri, Eğim Hesaplama, Kalkulator Nachylenia, Kalkulator Kemiringan.