How To Find Domain Of Inverse Function

Finding the Inverse of a Function (page 3 of 7)

Sections: Definition / Inverting a graph, Is the inverse a function?, Finding inverses, Proving inverses

The customary method of finding the inverse is some variant of the method I'g going to use beneath. Whatever method you use, brand sure y'all do the exact same steps in the exact same lodge every fourth dimension, so you remember those steps when you go to the test.

Observe the inverse of y = iiix � two .

Hither's how the procedure works:

Here's my original office:
Now I'll try to solve for " x = ":
Now I'll try to solve for " x = ":
Once I accept " x = ", I'll switch x and y ; the " y =" is the changed.

Then the inverse is y = ^{(x + 2)} / ₃

If you need to find the domain and range , look at the original function and its graph. The domain of the original function is the set of all allowable x -values; in this case, the function was a simple polynomial, then the domain was "all real numbers". The range of the original function is all the y -values you'll pass on the graph; in this case, the direct line goes on for ever in either management, so the range is also "all real numbers". To detect the domain and range of the inverse, just bandy the domain and range from the original role.

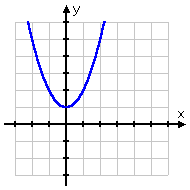
Find the inverse role of y = x ⁱⁱ + one , if it exists.

In that location will exist times when they give you lot functions that don't take inverses.

From the graph, it'southward easy to meet that this function can't possibly accept an inverse, since it violates the Horizontal Line Test:

function without an inverse function

Information technology is usually considered acceptable to describe the above graph, depict a horizontal line beyond it that crosses the graph twice, and then say something like "The inverse of this role is non itself a function, because of the Horizontal Line Exam". But some teachers want to see the algebra anyway. Exist sure to check with your teacher and verify what will be an acceptable answer -- and practice this before the examination! Copyright � Elizabeth Stapel 2000-2011 All Rights Reserved

What volition this await like when I try to observe the inverse algebraically? The Vertical Line Test says that I can't have two y 's that share an 10 -value. That is, each x has to have a UNIQUE corresponding y value. Merely look at what happens when I try to solve for " x = ":

My original function:
Solving for " x = ":
Solving for " x = ":

Well, I solved for " x = ", but I didn't get a UNIQUE " 10 = ". Instead, I've shown that whatever given x -value will actually correspond to ii unlike y -values, one from the "plus" on the square root and the other from the "minus".

The inverse is non a function.

Whatsoever time you come up with a "�" sign, you can be pretty sure that the inverse isn't a function.

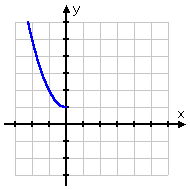
Find the inverse part of y = 10 ⁱⁱ + 1, x < 0 .

The only difference between this function and the previous one is that the domain has been restricted to simply the negative half of the ten -axis. This restriction makes the graph look like this:

y = 10^2 + 1, x <= 0

This office will have an changed that is also a function. Only well-nigh any fourth dimension they give you a problem where they've taken the trouble to restrict the domain, y'all should take intendance with the algebra and draw a nice picture, because the changed probably is a function, but it volition probably take some extra endeavor to prove this. In this instance, since the domain is x < 0 and the range (from the graph) is ane < y , then the inverse will accept a domain of one < ten and a range of y < 0 . Hither's how the algebra looks:

The original function:
Solve for " x = ":


By figuring out the domain and range of the inverse, I know that I should choose the negative sign for the foursquare root:
At present I'll switch the x and y ; the new " y =" is the inverse:

(The " x > 1 " restriction comes from the fact that x is inside a square root.)

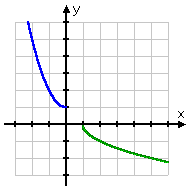
Then the changed is y = �sqrt(10 � 1), x > 1 , and this inverse is besides a function.

Here's the graph:

function and inverse function

<< Previous Pinnacle | 1 | 2 | three | 4 | 5 | 6 | vii| Return to Alphabetize Adjacent >>

Cite this article as:

Stapel, Elizabeth. "Finding the Inverse of a Function." Purplemath. Available from
https://world wide web.purplemath.com/modules/invrsfcn3.htm. Accessed